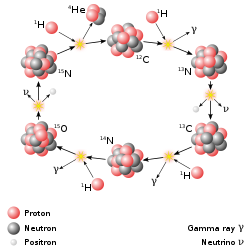A nuclear weapon is an explosive device that derives its destructive force from nuclear reactions, either fission or a combination of fission and fusion. Both reactions release vast quantities of energy from relatively small amounts of matter; a modern thermonuclear weapon weighing little more than a thousand kilograms can produce an explosion comparable to the detonation of more than a billion kilograms of conventional high explosive.
Thus, even single small nuclear devices no larger than traditional bombs can devastate an entire city by blast, fire and radiation. Nuclear weapons are considered weapons of mass destruction, and their use and control has been a major focus of international relations policy since their debut.
In the history of warfare, only two nuclear weapons have been detonated offensively, both near the end of World War II. The first was detonated on the morning of 6 August 1945, when the United States dropped a uranium gun-type device code-named "Little Boy" on the Japanese city of Hiroshima. The second was detonated three days later when the United States dropped a plutonium implosion-type device code-named "Fat Man" on the city of Nagasaki, Japan. These bombings resulted in the immediate deaths of around 120,000 people (mostly civilians) from injuries sustained from the explosion and acute radiation sickness, and even more deaths from long-term effects of ionizing radiation. The use of these weapons was and remains controversial.
Since the Hiroshima and Nagasaki bombings, nuclear weapons have been detonated on over two thousand occasions for testing purposes and demonstration purposes. A few states have possessed such weapons or are suspected of seeking them. The only countries known to have detonated nuclear weapons—and that acknowledge possessing such weapons—are (chronologically) the United States, the Soviet Union (succeeded as a nuclear power by Russia), the United Kingdom, France, the People's Republic of China, India, Pakistan, and North Korea. Israel is also widely believed to possess nuclear weapons, though it does not acknowledge having them.
Types of nuclear weapons

There are two basic types of nuclear weapon. The first type produces its explosive energy through nuclear fission reactions alone. Such fission weapons are commonly referred to as atomic bombs or atom bombs (abbreviated as A-bombs), though their energy comes specifically from the nucleus of the atom.
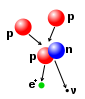
In fission weapons, a mass of fissile material (enriched uranium or plutonium) is assembled into a supercritical mass—the amount of material needed to start an exponentially growing nuclear chain reaction—either by shooting one piece of sub-critical material into another (the "gun" method), or by compressing a sub-critical sphere of material using chemical explosives to many times its original density (the "implosion" method). The latter approach is considered more sophisticated than the former, and only the latter approach can be used if plutonium is the fissile material.
A major challenge in all nuclear weapon designs is to ensure that a significant fraction of the fuel is consumed before the weapon destroys itself. The amount of energy released by fission bombs can range between the equivalent of less than a ton of TNT upwards to around 500,000 tons (500 kilotons) of TNT.
The second basic type of nuclear weapon produces a large amount of its energy through nuclear fusion reactions. Such fusion weapons are generally referred to as thermonuclear weapons or more colloquially as hydrogen bombs (abbreviated as H-bombs), as they rely on fusion reactions between isotopes of hydrogen (deuterium and tritium). However, all such weapons derive a significant portion – and sometimes a majority – of their energy from fission (including fission induced by neutrons from fusion reactions). Unlike fission weapons, there are no inherent limits on the energy released by thermonuclear weapons. Only six countries—United States, Russia, United Kingdom, People's Republic of China, France and India—have conducted thermonuclear weapon tests. (Whether India has detonated a "true," multi-staged thermonuclear weapon is controversial.)

Thermonuclear bombs work by using the energy of a fission bomb in order to compress and heat fusion fuel. In the Teller-Ulam design, which accounts for all multi-megaton yield hydrogen bombs, this is accomplished by placing a fission bomb and fusion fuel (tritium, deuterium, or lithium deuteride) in proximity within a special, radiation-reflecting container. When the fission bomb is detonated, gamma and X-rays emitted first compress the fusion fuel, then heat it to thermonuclear temperatures. The ensuing fusion reaction creates enormous numbers of high-speed neutrons, which then can induce fission in materials which normally are not prone to it, such as depleted uranium. Each of these components is known as a "stage," with the fission bomb as the "primary" and the fusion capsule as the "secondary." In large hydrogen bombs, about half of the yield, and much of the resulting nuclear fallout, comes from the final fissioning of depleted uranium.
By chaining together numerous stages with increasing amounts of fusion fuel, thermonuclear weapons can be made to an almost arbitrary yield; the largest ever detonated (the Tsar Bomba of the USSR) released an energy equivalent to over 50 million tons (50 megatons) of TNT. Most thermonuclear weapons are considerably smaller than this, due for instance to practical constraints in fitting them into the space and weight requirements of missile warheads.
There are other types of nuclear weapons as well. For example, a boosted fission weapon is a fission bomb which increases its explosive yield through a small amount of fusion reactions, but it is not a fusion bomb. In the boosted bomb, the neutrons produced by the fusion reactions serve primarily to increase the efficiency of the fission bomb. Some weapons are designed for special purposes; a neutron bomb is a thermonuclear weapon that yields a relatively small explosion but a relatively large amount of neutron radiation; such a device could theoretically be used to cause massive casualties while leaving infrastructure mostly intact and creating a minimal amount of fallout.
The detonation of a nuclear weapon is accompanied by a blast of neutron radiation. Surrounding a nuclear weapon with suitable materials (such as cobalt or gold) creates a weapon known as a salted bomb. This device can produce exceptionally large quantities of radioactive contamination. Most variety in nuclear weapon design is in different yields of nuclear weapons for different types of purposes, and in manipulating design elements to attempt to make weapons extremely small.
Nuclear strategy

Nuclear warfare strategy is a way for either fighting or avoiding a nuclear war. The policy of trying to ward off a potential attack by a nuclear weapon from another country by threatening nuclear retaliation is known as the strategy of nuclear deterrence. The goal in deterrence is to always maintain a second strike status (the ability of a country to respond to a nuclear attack with one of its own) and potentially to strive for first strike status (the ability to completely destroy an enemy's nuclear forces before they could retaliate). During the Cold War, policy and military theorists in nuclear-enabled countries worked out models of what sorts of policies could prevent one from ever being attacked by a nuclear weapon.
Different forms of nuclear weapons delivery (see below) allow for different types of nuclear strategy, primarily by making it difficult to defend against them and difficult to launch a pre-emptive strike against them. Sometimes this has meant keeping the weapon locations hidden, such as putting it on submarines or train cars whose locations are very hard for an enemy to track, and other times this means burying them in hardened bunkers.
Other responses have included attempts to make it seem likely that the country could survive a nuclear attack, by using missile defense (to destroy the missiles before they land) or by means of civil defense (using early warning systems to evacuate citizens to a safe area before an attack). Note that weapons which are designed to threaten large populations or to generally deter attacks are known as strategic weapons. Weapons which are designed to actually be used on a battlefield in military situations are known as tactical weapons.
There are critics of the very idea of nuclear strategy for waging nuclear war who have suggested that a nuclear war between two nuclear powers would result in mutual annihilation. From this point of view, the significance of nuclear weapons is purely to deter war because any nuclear war would immediately escalate out of mutual distrust and fear, resulting in mutually assured destruction. This threat of national, if not global, destruction has been a strong motivation for anti-nuclear weapons activism.
Critics from the peace movement and within the military establishment have questioned the usefulness of such weapons in the current military climate. The use of (or threat of use of) such weapons would generally be contrary to the rules of international law applicable in armed conflict, according to an advisory opinion issued by the International Court of Justice in 1996.
Perhaps the most controversial idea in nuclear strategy is that nuclear proliferation would be desirable. This view argues that, unlike conventional weapons, nuclear weapons successfully deter all-out war between states, and they are said to have done this during the Cold War between the U.S. and the Soviet Union. Political scientist Kenneth Waltz is the most prominent advocate of this argument.
It has been claimed that the threat of potentially suicidal terrorists possessing nuclear weapons (a form of nuclear terrorism) complicates the decision process. Mutually assured destruction may not be effective against an enemy who expects to die in a confrontation, as they may feel they will be rewarded in a religious afterlife as martyrs and would not therefore be deterred by a sense of self-preservation. Further, if the initial act is from rogue groups of individuals instead of a nation, there is no fixed nation or fixed military targets to retaliate against. It has been argued, especially after the September 11, 2001 attacks, that this complication is the sign of the next age of nuclear strategy, distinct from the relative stability of the Cold War.
Weapons delivery

Nuclear weapons delivery—the technology and systems used to bring a nuclear weapon to its target—is an important aspect of nuclear weapons relating both to nuclear weapon design and nuclear strategy. Additionally, developing and maintaining delivery options is among the most resource-intensive aspects of nuclear weapons: according to one estimate, deployment of nuclear weapons accounted for 57% of the total financial resources spent by the United States in relation to nuclear weapons since 1940.
Historically the first method of delivery, and the method used in the two nuclear weapons actually used in warfare, is as a gravity bomb, dropped from bomber aircraft. This method is usually the first developed by countries as it does not place many restrictions on the size of the weapon, and weapon miniaturization is something which requires considerable weapons design knowledge. It does, however, limit the range of attack, the response time to an impending attack, and the number of weapons which can be fielded at any given time.
Additionally, specialized delivery systems are usually not necessary; especially with the advent of miniaturization, nuclear bombs can be delivered by both strategic bombers and tactical fighter-bombers, allowing an air force to use its current fleet with little or no modification. This method may still be considered the primary means of nuclear weapons delivery; the majority of U.S. nuclear warheads, for example, are represented in free-fall gravity bombs, namely the B61.
More preferable from a strategic point of view are nuclear weapons mounted onto a missile, which can use a ballistic trajectory to deliver a warhead over the horizon. While even short range missiles allow for a faster and less vulnerable attack, the development of intercontinental ballistic missiles (ICBMs) and submarine-launched ballistic missiles (SLBMs) has allowed some nations to plausibly deliver missiles anywhere on the globe with a high likelihood of success.
More advanced systems, such as multiple independently targetable reentry vehicles (MIRVs) allow multiple warheads to be launched at several targets from any one missile, reducing the chance of any successful missile defense. Today, missiles are most common among systems designed for delivery of nuclear weapons. Making a warhead small enough to fit onto a missile, though, can be a difficult task.
Tactical weapons (see above) have involved the most variety of delivery types, including not only gravity bombs and missiles but also artillery shells, land mines, and nuclear depth charges and torpedoes for anti-submarine warfare. An atomic mortar was also tested at one time by the United States. Small, two-man portable tactical weapons (somewhat misleadingly referred to as suitcase bombs), such as the Special Atomic Demolition Munition, have been developed, although the difficulty to combine sufficient yield with portability limits their military utility.
Governance, control, and law

Because of the immense military power they can confer, the political control of nuclear weapons has been a key issue for as long as they have existed; in most countries the use of nuclear force can only be authorized by the head of government or head of state.
In the late 1940s, lack of mutual trust was preventing the United States and the Soviet Union from making ground towards international arms control agreements, but by the 1960s steps were being taken to limit both the proliferation of nuclear weapons to other countries and the environmental effects of nuclear testing. The Partial Test Ban Treaty (1963) restricted all nuclear testing to underground nuclear testing, to prevent contamination from nuclear fallout, while the Nuclear Non-Proliferation Treaty (1968) attempted to place restrictions on the types of activities which signatories could participate in, with the goal of allowing the transference of non-military nuclear technology to member countries without fear of proliferation.
In 1957, the International Atomic Energy Agency (IAEA) was established under the mandate of the United Nations in order to encourage the development of the peaceful applications of nuclear technology, provide international safeguards against its misuse, and facilitate the application of safety measures in its use. In 1996, many nations signed and ratified the Comprehensive Test Ban Treaty which prohibits all testing of nuclear weapons, which would impose a significant hindrance to their development by any complying country.
Additional treaties have governed nuclear weapons stockpiles between individual countries, such as the SALT I and START I treaties, which limited the numbers and types of nuclear weapons between the United States and the Soviet Union.
Nuclear weapons have also been opposed by agreements between countries. Many nations have been declared Nuclear-Weapon-Free Zones, areas where nuclear weapons production and deployment are prohibited, through the use of treaties. The Treaty of Tlatelolco (1967) prohibited any production or deployment of nuclear weapons in Latin America and the Caribbean, and the Treaty of Pelindaba (1964) prohibits nuclear weapons in many African countries. As recently as 2006 a Central Asian Nuclear Weapon Free Zone was established amongst the former Soviet republics of Central Asia prohibiting nuclear weapons.
In the middle of 1996, the International Court of Justice, the highest court of the United Nations, issued an Advisory Opinion concerned with the "Legality of the Threat or Use of Nuclear Weapons". The court ruled that the use or threat of use of nuclear weapons would violate various articles of international law, including the Geneva Conventions, the Hague Conventions, the UN Charter, and the Universal Declaration of Human Rights.
Additionally, there have been other, specific actions meant to discourage countries from developing nuclear arms. In the wake of the tests by India and Pakistan in 1998, economic sanctions were (temporarily) levied against both countries, though neither were signatories with the Nuclear Non-Proliferation Treaty. One of the stated casus belli for the initiation of the 2003 Iraq War was an accusation by the United States that Iraq was actively pursuing nuclear arms (though this was soon discovered not to be the case as the program had been discontinued). In 1981, Israel had bombed a nuclear reactor in Osirak, Iraq, in what it called an attempt to halt Iraq's previous nuclear arms ambitions.[citation needed]
Disarmament
Beginning with the 1963 Partial Test Ban Treaty and continuing through the 1996 Comprehensive Test Ban Treaty, there have been many treaties to limit or reduce nuclear weapons testing and stockpiles. The 1968 Nuclear Non-Proliferation Treaty has as one of its explicit conditions that all signatories must "pursue negotiations in good faith" towards the long-term goal of "complete disarmament". However, no nuclear state has treated that aspect of the agreement as having binding force.
Only one country—South Africa—has ever fully renounced nuclear weapons they had independently developed. A number of former Soviet republics—Belarus, Kazakhstan, and Ukraine—returned Soviet nuclear arms stationed in their countries to Russia after the collapse of the USSR.
Uses
Apart from their use as weapons, nuclear explosives have been tested and used for various non-military uses, and proposed, but not used for large scale earth moving. When long term health and clean-up costs were included, there was no economic advantage over conventional explosives.
Synthetic elements, such as einsteinium and fermium, created by neutron bombardment of uranium and plutonium during thermonuclear explosions, were discovered in the aftermath of the first thermonuclear bomb test. In 2008 the worldwide presence of new isotopes from atmospheric testing beginning in the 1950s was developed into a reliable way of detecting art forgeries, as all paintings created after that period contain traces of cesium-137 and strontium-90, isotopes that did not exist in nature before 1945.
Nuclear explosives have also been seriously studied as potential propulsion mechanisms for space travel

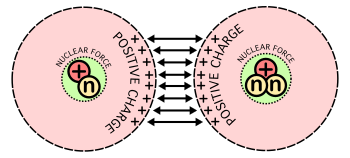
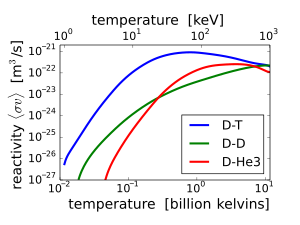

 increases from virtually zero at room temperatures up to meaningful magnitudes at temperatures of
increases from virtually zero at room temperatures up to meaningful magnitudes at temperatures of